Acing AP Calculus BC: Strategies for Integration and Differentiation

                         

Welcome, AP Calculus BC students! As you embark on your journey to conquer the AP Calculus BC exam, mastering integration and differentiation is crucial. In this blog post, we'll explore essential strategies and tips to help you excel in these fundamental concepts.

Understanding Integration

Integration is all about finding the area under a curve and, in many ways, the reverse of differentiation. To ace integration, remember these key points:

                               

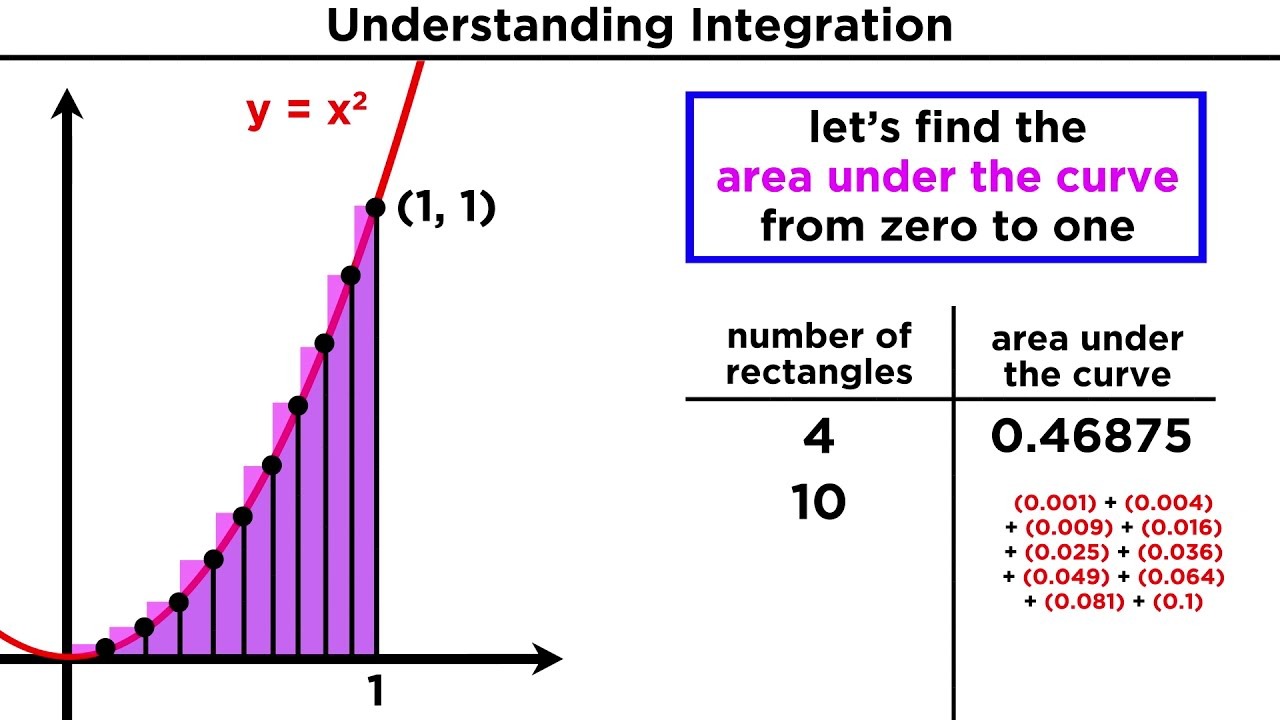
1. Review Basic Integration Techniques: Begin by revisiting the power rule, constant multiple rule, and simple integration formulas. These are the building blocks for more complex integration problems.
2. Differentiate Between Definite and Indefinite Integrals: Understand the difference between definite and indefinite integrals. Definite integrals yield a specific numeric result, while indefinite integrals provide an antiderivative (also known as the primitive function).
3. Practice, Practice, Practice: Work through a variety of integration problems, starting with simple ones and gradually advancing to more challenging ones. Regular practice is the key to gaining confidence in integration.

Mastering Differentiation

Differentiation is at the core of calculus, allowing us to analyze rates of change and slopes of curves. To become proficient in differentiation, follow these steps:

                                                   

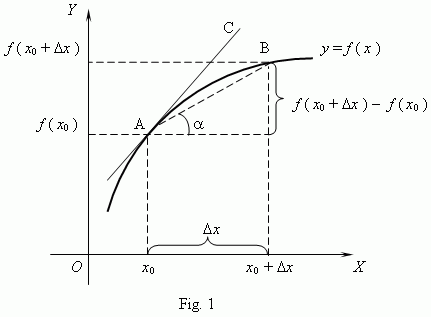
1. Revisit Differentiation Concepts: Review the fundamental rules, such as the chain rule, product rule, and quotient rule. Understanding these rules is essential for handling complex functions.
2. Identify Functions Requiring Specific Techniques: Practice identifying which differentiation technique to apply to various functions. Recognizing when to use the chain rule or the product rule can save you valuable time during the exam.
3. Engage in Step-by-Step Problem Solving: Work through a range of differentiation problems step by step. Familiarize yourself with common functions and their derivatives.

Integration Strategies

Integration can sometimes be tricky, especially with complex functions. Employ the following strategies to tackle challenging integration problems:

                                         

1. Trigonometric Substitutions: Use trigonometric substitutions to simplify integration, especially when you encounter square roots of trigonometric expressions.
2. Trigonometric Substitutions: Master the technique of integration by parts to handle products of functions. This method can help you integrate complicated expressions effectively.
3. Recognize When to Use u-Substitution: Understand when to apply u-substitution, which involves choosing a new variable to simplify an integral. This technique is often helpful with more complex integrals.

Differentiation Strategies

As you encounter more complex functions in the exam, these differentiation strategies will prove invaluable:

                                           

1. Implicit Differentiation: Practice differentiating implicit functions, where the dependent and independent variables are intertwined. This skill is essential for handling curves represented implicitly.
2. Inverse Trigonometric Functions: Be comfortable with differentiating inverse trigonometric functions. Recognize their derivatives and apply them effectively in calculus problems.
3. Trigonometric and Exponential Functions: Master differentiating trigonometric and exponential functions. These functions frequently appear in calculus, and familiarity with their derivatives is crucial.

Optimization and Applications

Calculus extends beyond theory and plays a vital role in solving real-world problems. Here's how you can apply integration and differentiation in practical scenarios:

1. Applications of Integration: Understand how to use integration to find areas, volumes, and even the average value of functions. Real-life problems involving rates of change and accumulation are common in the AP Calculus BC exam.
                                
2. Optimization Problems: Learn to apply differentiation to optimize functions. These problems involve finding maximum and minimum values, which have many real-world applications.
                               

Test-Taking Tips

In addition to mastering calculus concepts, excel in the exam with these test-taking strategies:

1. Manage Your Time: During the exam, allocate your time wisely. Work through questions you find easier first and leave more challenging ones for later.
                                 
2. Stay Calm and Focused: Stay composed and focused during the exam. Read questions carefully, and avoid second-guessing yourself too much.
                                 
3. Strategic Question Approach: Strategically approach multiple-choice questions, considering the options and eliminating clearly incorrect answers.
                                  

Additional Resources

To enhance your understanding and practice, utilize these resources:

1. Textbooks and Online Tutorials: Refer to reputable calculus textbooks and online tutorials for additional explanations and practice problems.
                              
2. Practice Tests: Take full-length practice tests regularly to simulate the exam experience and identify areas for improvement.
                             

Conclusion

By implementing these strategies and practicing consistently, you'll build confidence in your calculus skills and be well-prepared to excel in the AP Calculus BC exam. Remember, understanding integration and differentiation is essential for many future STEM pursuits. Best of luck in your preparation, and remember that we are here to support your journey every step of the way!